Calculate an estimate of x-ray dose rate from an x-ray tube given kV and mA
Published: Mar 24, 2024
Source: Dr Chris Robbins, Grallator/ Ionactive Radiation Protection Resource
Prelim
The most meaningful way of determining the dose rate output of an x-ray tube is to measure it - perhaps using a tissue equivalent ion chamber in a purpose made shielded enclosure. Determining beam quality is something you might see take place during medical physics procedures (i.e. for diagnostic radiology or x-ray therapeutic equipment). Real time measurements however may not be possible - so where next?
The next most likely reliable resource will be the manufacturer data sheets. However, in many cases the data provided will be in terms of TVT (10th value thickness) or HVT (1/2 value thickness) of a certain material (e.g. steel) at a certain kV (this is particularly the case for suppliers of industrial radiography NDT x-ray equipment). This might be all your need, but what if you need to consider enclosure shielding design - information on the output (dose rate) of the x-ray tube at maximum kV / mA becomes important.
[Ionactive comment: Without x-ray tube output data some reasonable assumptions can be made - but we would never rely on this alone. For example, take a 150 kVp x-ray tube in an enclosure at a certain distance from a shielding wall (assume it is pointing directly at this wall - so worse case). For 150 kV we can see from data tables (search Ionactive!), that the TVT for lead will be about 1 mm. Assume we need at least 7 TVT in the wall (a reasonable first guess). That will provide an attenuation of 10-7 (7 mm lead). If we want no more than 1 micro Gy/h on the outside of the wall (= 1 micro Sv/h for purposes of this article), then we can afford a dose rate - on the inner surface of the wall - of between 1-10 Gy/h and we will still meet our shielding objective. If the x-ray tube is 2 m from the inner wall (for example), then the dose rate output at 1 m could be in the region of 4-40 Gy/h and our shielding assumption would still work. Of course there are other factors here - such as, could the mA be increased above our assumption, and what about filtration, could this harden the x-ray beam and shift the average energy upwards?. Lots of things to consider! However, those that know typical x-ray tube outputs, based on years of experience, might use this type of analysis for a back of envelope calculation].
If no output data is available then you have to try something else. This is not that unusual - in one recent piece of client work based on military hardware, we were only given the max kV and mA.
You can try turning to older data - we have featured loads of this on our website - such as here: X-ray equipment: Constant potential 50-200 KV (opens in a new window so you can read with this article). If you visit this resource, based on BS4094, you will see the following data for 150kV (with minimal filtration) - 5 R / mA per minute at 1 m. With conversion (explained at the above link), this is equivalent to 2.63 Gy/h at 1 m at 1 mA. Note that this is between 1 and 40 Gy/h which was noted above - so the right ballpark. Note from the linked resource that this is with minimal filtration so near a likely maximum for modern day x-ray tube applications (where 2-3 mm equivalent Al filtration might be use). Where the inherent filtration is minimal, perhaps in the case of a NDT industrial radiography set, it is likely that copper / steel / lead would be used as an external filter, however this might not be reliable when considering enclosure shielding (since in this case external filtration is influenced by human factors).
So what other options might we have? Computer models have their place (and more of that in a further Ionactive article soon).
The option we will now choose is the back of the envelope ballpark calculation from first principles. And for this we turn to our colleague and friend Dr Chris Robbins (of Grallator) who will now take us through the maths and physics. If you want to experience the following resource in an interactive widget, then head over to X-ray Tube Dose Rate Calculator Widget.
An estimate of X-ray dose rate
Dr Chris Robbins, Grallator
An X-ray machine is a device for producing energetic and penetrating photons by accelerating elections in a strong electric field
and colliding them with a target.
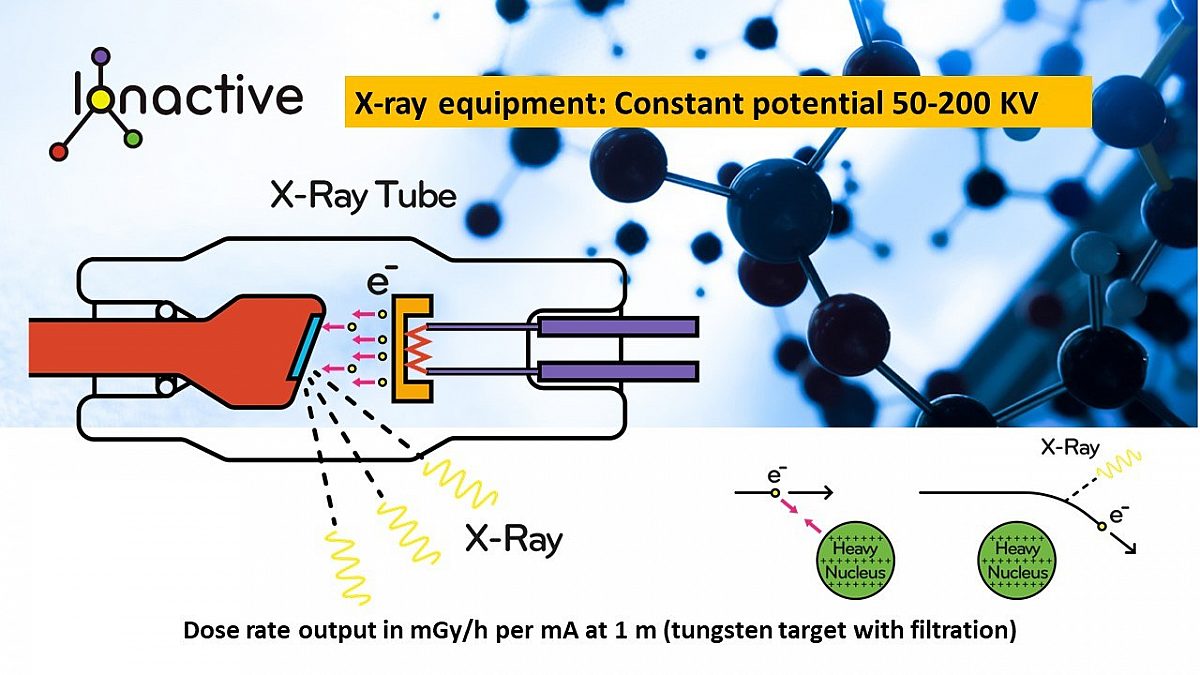
This note gives a back-of-the-envelope estimate of the dose rate received by a a person in \(Gy hr^{-1}\) at a distance \(r\) metres from the source, \(D_{Gy hr^{-1}} (r) \).
Calculating the power
The dose rate is a measure of absorbed energy per unit mass per unit time. The absorption part will be detailed later, so this first part will look at the power, or energy per unit time.
The diagram above is essentially an electrical circuit. A current, \(I\), of electrons flows through a vacuum from the cathode on the right to the target anode on the left due to electric field created by the applied potential difference, \(V\), between the anode and cathode. This electric field accelerates the electrons so that they gain an energy, \(E\).
The power of the electron beam, \(P_b\) is given by the standard electrical circuit expression \(P_b=IV\) in watts (W) or equivalently J/s.
The energy of the electron as it hits the target is given by \(E=V\) in electron volts.
Most of the energy of the electrons deposited goes in to heating the target. However, a fraction is released as X-rays. These X-rays can be produced as a result of a change of velocity (Bremsstrahlung), or by interacting with electrons in the atoms of the target material (Characteristic X-rays). The details and differences are not used in this exercise and the important point is that an estimate of the fraction of the total power that is converted to X-rays is required. It turns out that this fraction is related to the energy of the electrons, \(E\), and the atomic number of the target material, \(Z\), and can be approximated as \[ F_e = 1 \times 10^{-6} Z E \] where \(E\) is in units of keV, and \(Z\) is a number.
Putting all the above together, the approximate X-ray power is given by \[ P_{X,Js^-1} = P_b \cdot F_e \] or, converting the time unit to hours by \[ P_{X,Jhr^-1} = 3600 \cdot P_b \cdot F_e \]
Calculating the power density per unit area
At a distance \(r\) from the source, the energy released is spread over the surface of a sphere of radius \(r\), which has an area of \(4 \pi r^2\). The power per unit area at a distance \(r\) is therefore given by \[ \begin{align} P_{X,Jhr^-1 \cdot m^{-2}} &= \frac{3600 \cdot P_b \cdot F_e}{4\pi r^2} \\ \\ &= \frac{900 \cdot P_b \cdot F_e}{\pi r^2} \\ \\ &= \frac{900 \times 10^{-6} \times I V Z E}{\pi r^2} &= \frac{9 \times 10^{-4} \times I V Z E}{\pi r^2} \end{align} \] where
\(\quad\) \(I\) \(\quad\) is the beam current in amps, A
\(\quad\) \(V\) \(\quad\) is the device voltage in volts, V
\(\quad\) \(Z\) \(\quad\) is the target atomic number
\(\quad\) \(E\) \(\quad\) is the electron energy in KeV. \(E=V \times 10^{-3}\)
Using the last relationship leads to the further simplification of
\[\begin{align}P_{X,Jhr^-1 \cdot m^{-2}} &= \frac{9 \times 10^{-7} \times I V^2 Z}{\pi r^2}\end{align}\]
The above is just the inverse square law.
Note, the above does not take in to account any absorption in air, and this will be ignored here as negligible for the energies of interest.
Energy absorption rate at measuring point
At the measuring point we wish to calculate the energy absorbed per unit time per kg of matter (air, tissue, etc.). This has been described in detail in a different post (D=ME/6r2 Gamma dose rate formula) and will not be repeated here. The important result is that the absorbed energy rate in \(Gyhr^{-1}\) is approximated by multiplying the power per unit area by the mass energy attenuation coefficient \( ({\mu}/{\rho}) \) in units of \( m^2 kg^{-1}\), \[ D_{Gy hr^{-1}} = \frac{9 \times 10^{-7} \times I V^2 Z}{\pi r^2} \left( { \frac {\mu}{\rho}} \right) \]
An example
Consider an X-ray tube with the following characteristics:
\(\quad\) \(I=1 mA \quad (=1 \times 10^{-3} A) \)
\(\quad\) \(V=150 kV \quad (=150 \times 10^{3} V) \)
\(\quad\) \(Z=74 \quad (\mathrm{Tungsten \space target}) \)
\(\quad\) \(r=1 m \)
Substituting values into the above gives a [rounded] dose rate of
\[D_{Gy hr^{-1}} = 477 \left( { \frac {\mu}{\rho}} \right)\]
To give a value we need a value for \( ({\mu}/{\rho}) \). As a previous note pointed out (D=ME/6r2 Gamma dose rate formula), the value depends on the energy of the photon being absorbed and the material absorbing it, and correctly should take account of the full spectrum of possible energy values. That's a lot of detail for a back-of-the-envelope calculation! To simplify things, an assumption will be made that the value for \( ({\mu}/{\rho}) \) will be taken as the point value at the average energy of the X-rays produced, and the average energy for a 150 keV tube is taken as \(E_{ave} = 57.3\) keV (approx 1/3).
For the above, \(E_{ave} = 57.3\) keV, the mass energy absorption coefficient for soft tissue is \(3.52 \times 10^{-3} \space m^{2}kg^{-1} \). This gives a dose rate of \[ D_{Gy hr^{-1}} = 477 \times 3.52 \times 10^{-3} = 1.7 \space Gy hr^{-1} \]
This value is broadly of similar size to the 2.1 \(Gy hr^{-1}\) value given by the "SpekCalc" computer model and the BS 4094 value of 2.63 \(Gy hr^{-1}\).
The above value is for soft tissue, however, the body also has bones in it, so what is the dose rate for bone? Bone is denser than soft tissue and so has a higher mass energy absorption coefficient of \(1.59 \times 10^{-2} \space m^{2}kg^{-1} \). This gives a dose rate of \[ D_{Gy hr^{-1}} = 477 \times 1.59 \times 10^{-2} = 7.6 \space Gy hr^{-1} \] This value is higher than the previous result, and the BS 4094 value. However, a body is not 100% bone in the same way it is not 100% soft tissue! Taking a value of between 10 and 15% of body mass as bone, the weighted average dose rate is between \[ D_{Gy hr^{-1}} = (0.9 \times 1.7) + (0.1 \times 7.6) = 2.3 \space Gy hr^{-1} \] \[ \mathrm{and} \] \[ D_{Gy hr^{-1}} = (0.85 \times 1.7) + (0.15 \times 7.6) = 2.6 \space Gy hr^{-1} \] This is somewhere between the "Spekcalc" value and the BS 4094 value. In actuality, the "correct" value should take account of absorption in all the tissue and bone types, and should take full account of the spectrum of X-rays produced as absorption is sensitive to photon energy. Overall though, this back-of-the-envelope calculation gives good ball-park agreement.
Note, air has an absorption coefficient of \(3.29 \times 10^{-3} \space m^{2}kg^{-1} \) which is slightly smaller than the value for soft tissue. This gives a dose rate of \[ D_{Gy hr^{-1}} = 477 \times 3.29 \times 10^{-3} = 1.6 \space Gy hr^{-1} \]
Using the above results with shielding
The analysis above clearly shows that the nature of the absorbing medium is important when making such calculations. If we look at the range of values calculated, and include those obtained from the BS standard (and the quoted Spekcalc) value, they are from 1.6 Gy/h to 2.63 Gy/h. Note that this range includes absorbed dose averaging over tissue and bone as described above. Considering this range represents 3 different x-ray tube output references (including the x-ray tube calculations), they are remarkably similar.
