The inverse square law applies to any process which radiates out from a point in space (see Point Source and Fluence Rate to expand on this concept). With respect to Radiation Protection, the law says if you double your distance from a source of Ionising Radiation you will reduce your exposure by 4. It follows that if you triple your distance from the source, the exposure will reduce to 1/9 of the original value. This concept is one of the cornerstones of radiation protection and is used with the Distance Rule. It is not always reliable where the distance between source and measurement position is small compared to the size of the source. Generally, the rule will work mathematically where the distance between the source and the calculation point, is at least 10 times the largest dimension of the source.

If r is the distance from the source, the dose dose (or dose rate) D is proportional to 1/r² as shown below.

\[\text{ D (Dose or Dose rate)}\propto \frac{1}{r^{2}}\]

This can be expanded to consider two dose rates at two different distances in the following form:

\[\frac{D_{1}}{D_{2}}=\frac{r_{2}^{2}}{r_{1}^{2}}\]

Here D₁ is dose rate at distance r₁ and D₂ is dose rate at r₂ (some greater distance from the source). This can be rearranged in several ways, the example below allows us to find D₂ if we known D₁ and both distances r₁ and r₂ .

\[ D_{2}=D_{1}\frac{(r_{1})^{2}}{(r_{2})^{2}}\]

The graphic below is from our radiation protection widget resource where you can see this process interactively.

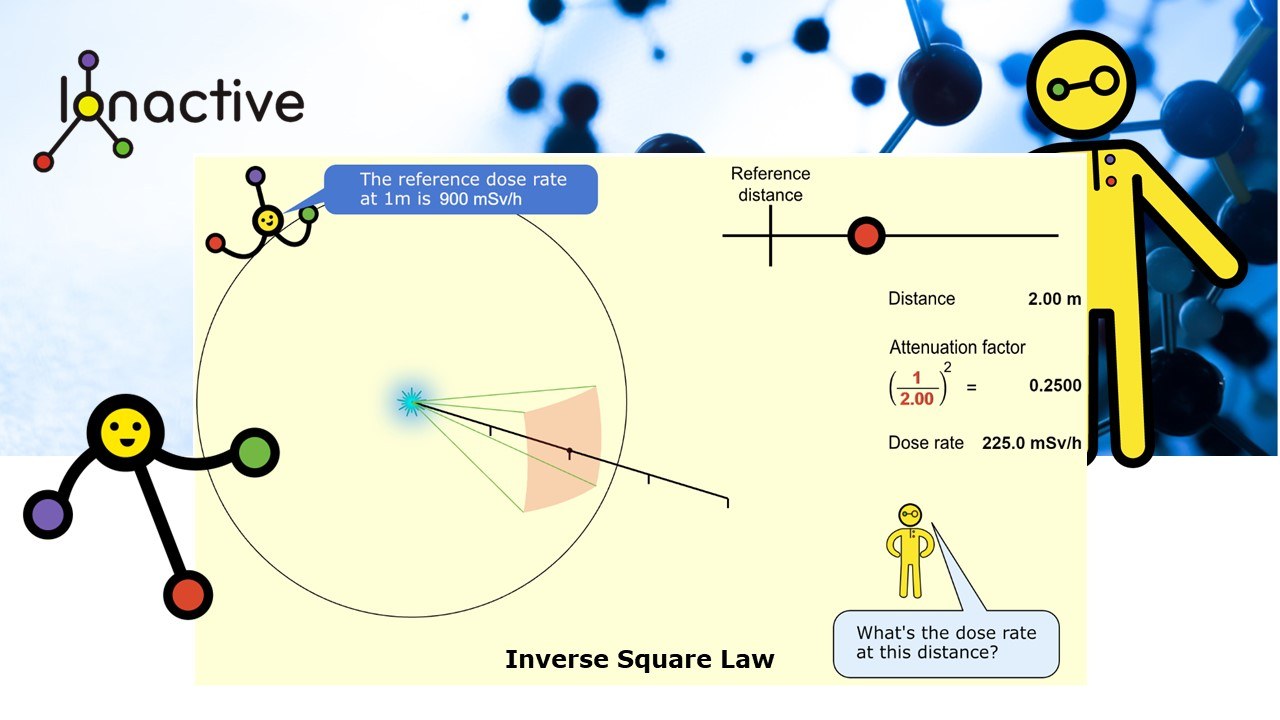
Try out the inverse square law widget now!

[Updated March 2024]