When \(1/d^2\) breaks down - part 1: line source
Published: Mar 22, 2024
Source: Dr Chris Robbins, Grallator
When \( 1/d^2 \) breaks down - part 1: line source
Dr Chris Robbins, Grallator
A point source of radiation will give an intensity reading that falls with distance as \( 1/d^2 \). Real sources are not point sources and have physical extent. For large distances the variation of intensity with distance will follow the \( 1/d^2 \) rule, however when the measurement distance is comparable with the physical dimensions this rule will break down due to geometry effects. This note considers these effects.
Consider a radioactive line source extending between \(–L\) and \(+L\) along the vertical axis.
The line source has an activity of \(S_L\) per unit length. (This example uses a line that has no extent in the \(x\) and
\(z\) axes. Full \(3d\) analysis will yield a broadly similar but more complicated result due to self-attenuation and
other \(3d\) effects.)
We seek to evaluate the intensity at a point
\(D\), a distance \(d\) along the horizontal axis, as shown below.
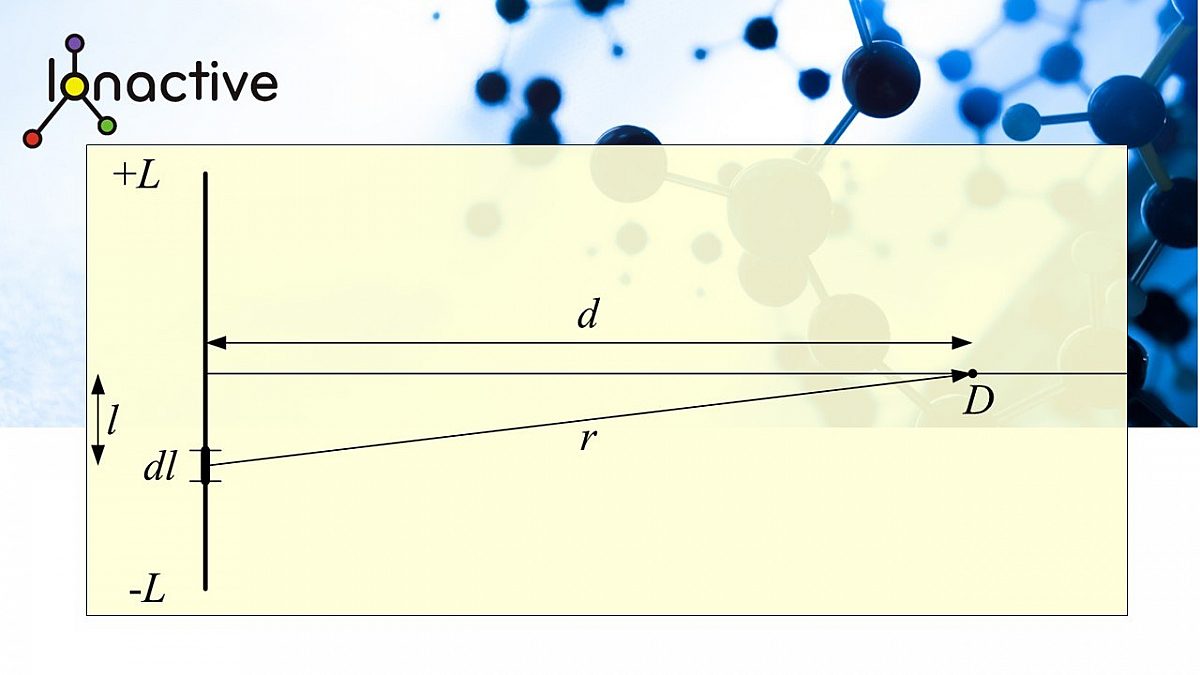
The small element \(dl\) is centred at \(l\) and gives a contribution to the total intensity at \(D\) by the inverse square law of \[ dS = \frac{S_L dl}{r^2} \] The total intensity, \(S\) at \(D\) is given by integrating all the contributions: \[ dS = \int^{+L}_{-L} \frac{S_L dl}{r^2} \] To solve this, use \(r^2=d^2+l^2\) and substitute \(x= \left( l/d \right)\) to get \[ S=\int^{+L}_{-L} \frac{S_L dl}{r^2} = \int^{+L}_{-L} \frac{S_L dl}{d^2+l^2} = \frac{S_L}{d} \int^{+L/d}_{-L/d} \frac{dx}{1+x^2} = \frac{2 S_L}{d} \mathrm{arctan} \left( \frac{L}{d} \right) \]
To study this further we use an expansion for \( \mathrm{arctan} \left( x \right) \): \[ \mathrm{arctan} \left( x \right) = x - \frac{x^3}{3} + \frac{x^5}{5} - \cdots \] so that \[ \begin{align} S &=\frac{2 S_L}{d} \left[ \frac{L}{d} - \frac{L^3}{3d^3} + \frac{L^5}{5d^5} - \cdots \right] \\ \\ &=\frac{2 S_L L}{d^2} - \frac{2 S_L L^3}{3d^4} + \frac{2 S_L L^5}{5d^6} - \cdots \end{align} \] We note that \(S\) follows a \(1/d^2\) relationship to first order and that the total intensity is related to the length multiplied by the emission per unit length as expected. It is also seen that there are corrections from higher-order terms. These corrections become smaller as the ratio \(L/d\) decreases. Say that we want a correction in the expansion of \(\mathrm{arctan}(x)\) of 1 part in 100 which approximately occurs when \[ \frac{L}{d} \approx 100 \times \frac{L^3}{3d^3} \Rightarrow \frac{L^2}{d^2} = \frac{3}{100} \space \space \mathrm{or} \space \space \frac{d}{L}=\frac{10}{\sqrt{3}} \approx 6 \] i.e. \(d\) is about 3 times the total length of the line source (remember the source has extent from \(–L\) to \(+L\) so has a total length of \(2L\)).
What does this mean practically?
The above gives a relationship between distance and intensity that is related to the \(\mathrm{arctan}\) function. What happens if a single reference reading is taken at a distance from the extended line source which is then used in a \(1/d^2\) calculation?
To look at this we'll use: \[\quad L = 1 \quad \mathrm{arbitrary \space distance \space units} \] \[\quad S_L = 1 \quad \mathrm{arbitrary \space activity \space units} \] and \(d\) will range from 1 to 30 distance units.
Case 1: reference reading at 1 distance unit
A reference reading at 1 distance unit will give the correct intensity of \(1.571\). This is close to the source so effects from the physical length of the source will be important in determining this reading, and in particular, the path travelled from the ends of the source to the measurement point is greater than the path from the centre of the source. As you move away from the source these physical effects reduce and the source approximates more closely to a point source. Applying a \(1/d^2\) calculation as you move away from the source reveals that the predicted values in this case will be lower than actual values because the original reading underestimates the total point-source intensity.
Case 2: reference reading at 20 distance units
A reference reading at 20 distance units will give the correct intensity of \(4.996 \times 10^{-3}\). This distance is 10 times the physical dimensions of the source, and so any effects arising from the physical extent of the source should be relatively small, and it should approximate to a point source. As you move away from the source a \(1/d^2\) calculation will give good results because of this. However, as you move closer, the effects of physical extent of the source will become apparent. Very close to the source, the \(1/d^2\) calculation will over-predict the intensity because it does not allow for the longer path length from the ends of the source.
The results of a \(1/d^2\) calculation using the above two reference points is shown in the plot below.

The following is concluded
- Taking a reference measurement very near the source results in a \(1/d^2\) model under-predicting intensity at larger distances.
- Taking a reference measurement at a larger distance from the source results in a \(1/d^2\) model over-predicting intensity at smaller distances.
Head over to part 2: area source for more radiation protection mathematics!
