Skyshine – radiation scattering around and over shielding

Unlike some of our other rules of thumbs, this article will take a slightly different approach by providing some insight into the issue, rather than a simple expression to calculate the effect (there are no such expressions that can be readily used to cover all source types and geometries). We will first express a simple rule of thumb and then delve into some data so you get an idea of how significant skyshine can be.

The rule of thumb: When considering radiation shielding for x-ray / gamma sources, don’t ignore radiation that might be scattering under, over or around the shielding. To do so can create quite embarrassing unexpected dose rates some distance away from the shielding!

Skyshine – visualising the problem (1)

Consider the following diagram. It depicts a radiation source of some type behind a shield (right hand side). The left-hand side represents a dose measurement point (a person). At this stage we do not need to consider height or shielding thickness, but we will assume the shielding is on firm dense ground and is infinitely wide (so we do not need to consider scattering under or around the sides of the shield, only above it).

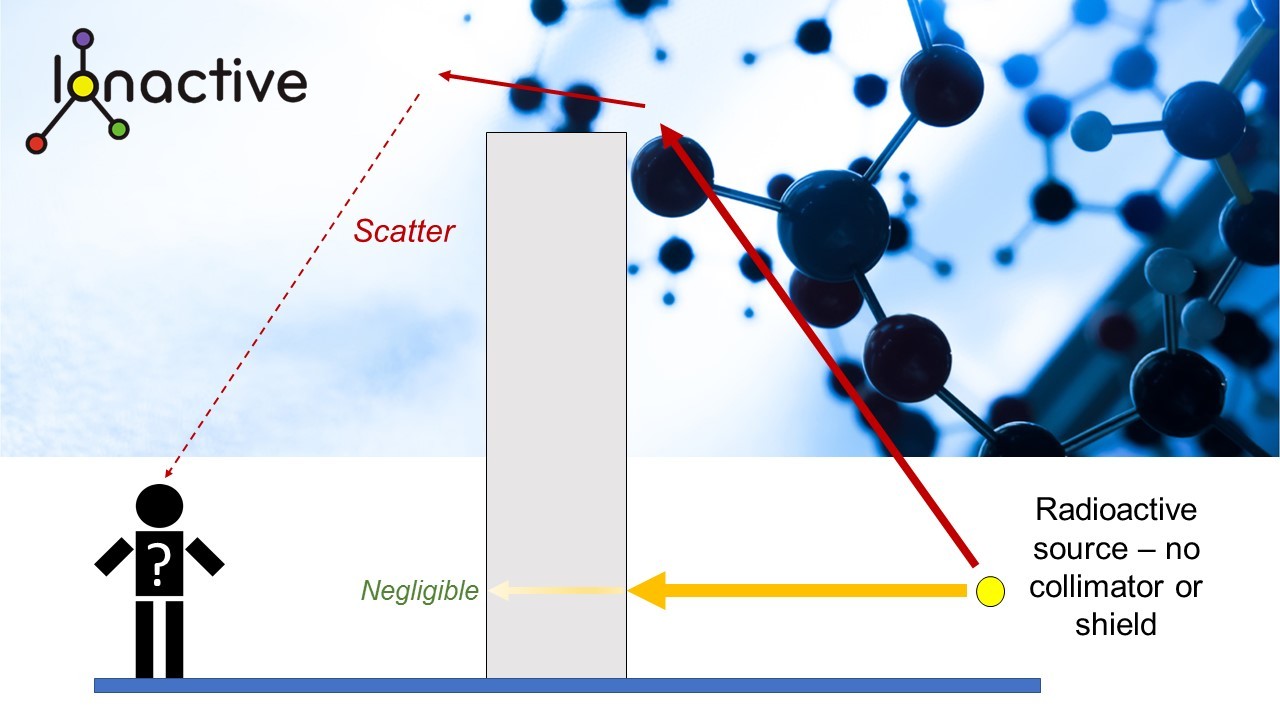
Therefore, there are two modes for radiation to arrive at the measurement point – through the wall or over the top of the shield. Experience using real measurements has shown that it is quite possible to measure negligible dose rates close up to the shield (if the shielding provides adequate attenuation) but which increases as you move back from the shielding, reaching a peak before reducing with further increase in distance. This is Skyshine. Whilst Skyshine will be worst where there is no shielding ‘above’ the source (i.e. a radiation bunker with no top shielding), it can still be significant if only modest top shielding is use (perhaps because it is assumed no one will have access above the source).

Skyshine – visualising the problem (2)

Before looking at real sources, distances and dose rates, its often useful to try and imagine what is going on by replacing the radiation source with a very bright high intensity beam of visible light aimed downwards onto the floor. In the picture below we have a similar setup, now using a torch beam and all other sources of light are removed (any building windows are blacked out etc). Now stand right next to the wall and look at your hands. What do you see (can you see them at all?). Now move away from the wall and look around – what do you think you would ‘see’? Probably illumination from over the wall and quite possibly more of your hands. By the wall you were in a shadow, away from it you are not. Its not a perfect translation of physics between visible light and gamma / x-rays, but its good enough to visualise Skyshine.

Example – Shielding Ir-192 with a wall, analysis of skyshine potential

For this analysis we are going to make the following assumptions / decisions.

• The source is Ir-192 with an activity of 740 GBq
• The source is not collimated
• Regardless of source position, the wall will provide shielding such that the surface dose rate is < 1 micro Sv/h (calculated).
• The wall is 4m in height
• Its width is infinite (this simplifies analysis and is similar to where you have a four walled bunker)
• The wall shielding material is irrelevant

With the above accepted we can now add some dimensions to the source diagram and shown below.

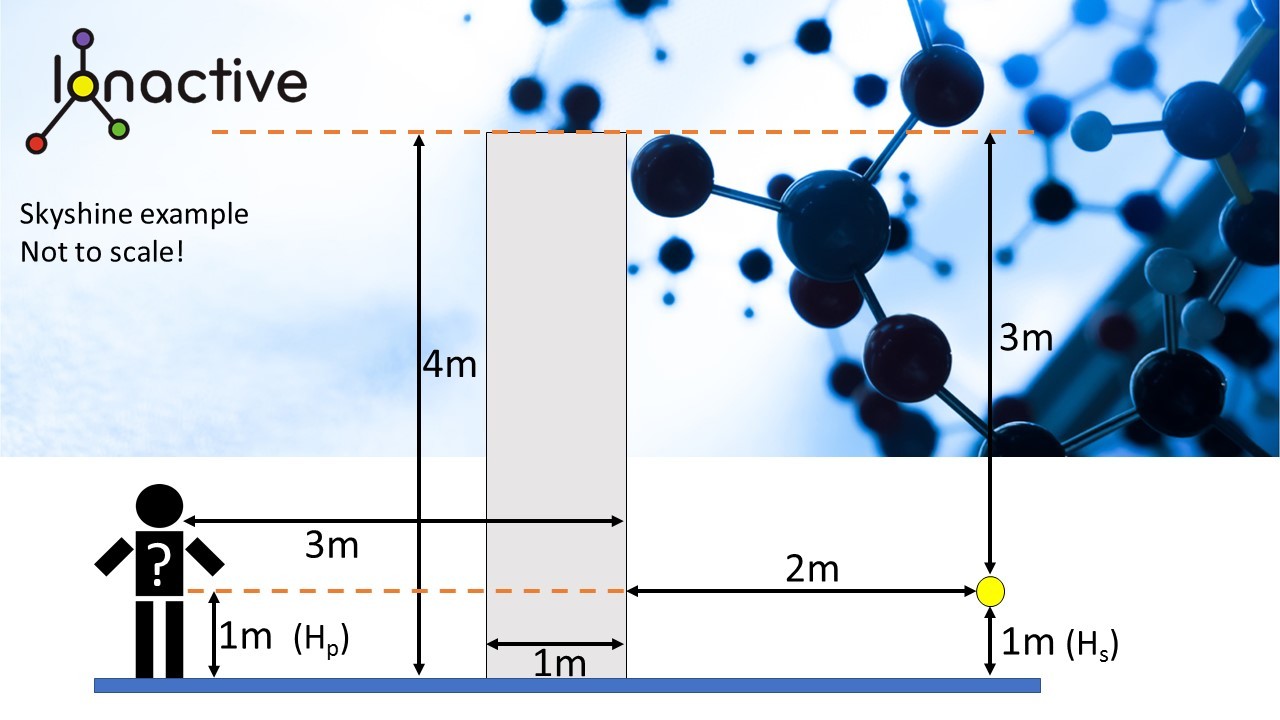
We will now use the Groves MicroSkyShine code to evaluate the dose to the person (Hp) in micro Sv/h. The diagram below is a depiction of the data in MicroSkyShine, but the intention of this rules of thumb resource is not to delve into this industry standard modelling software, but rather look at the at the results.

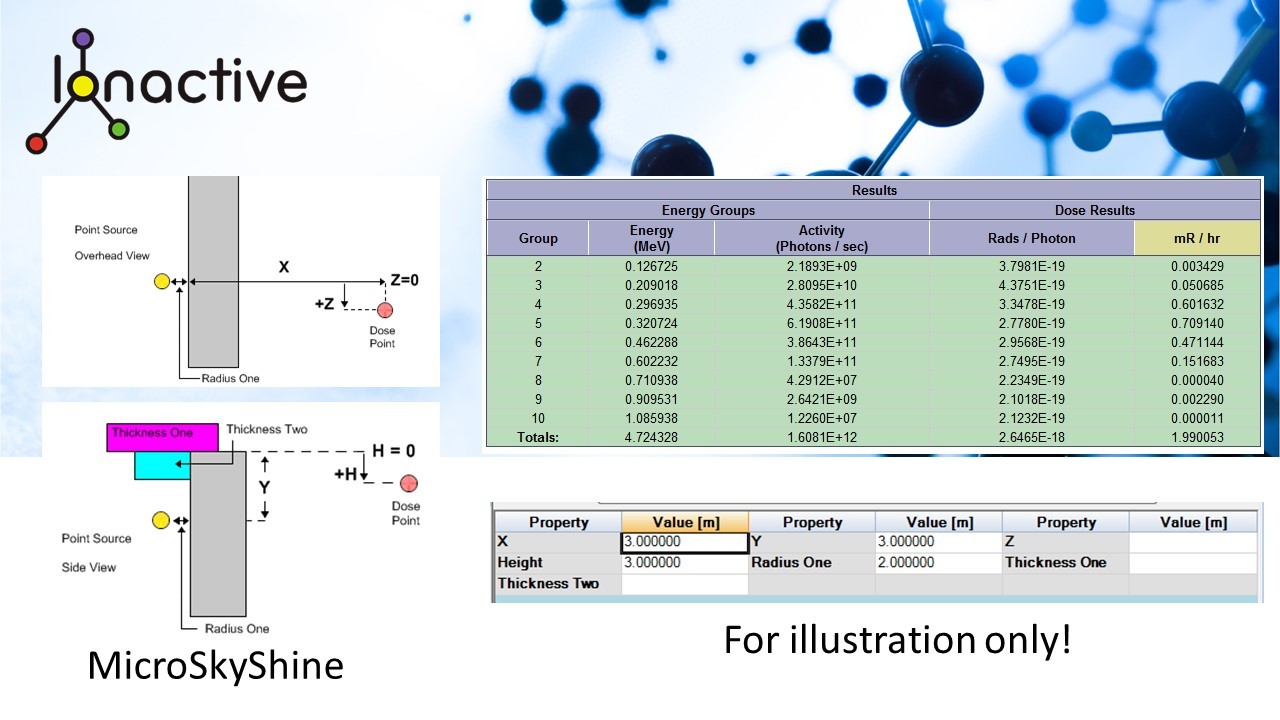
The results are in mR/h and the results in the above table show this to be 1.99 mR/h. We have then rounded this and converted this to micro Sv/h (using 1R = 0.877 Gy in air). The result is 18 micro Sv/h.

So, let us pause…

• The source is fully shielded behind the wall, the surface dose rate is < 1 micro Sv/h on the wall (we assume this is calculated as we cannot isolate the wall dose rate from any skyshine)
• The source is low down (1m from the floor)
• The person is 2m from the wall (i.e. 3m from the inner surface of the wall) and is low down (waist height dose point taken to be 1m from the floor)

Despite the above seemingly ‘safe’ geometry, the dose rate is of the order of 18 micro Sv/h, significantly more than the < 1 micro Sv/h expected on the wall surface. That is Skyshine!

Skyshine – the effect of moving nearer to, or further from the source

Forget using the inverse square law, it will not work. Furthermore, any assumption that a ‘calculated’ shield will perform as required if the facility has an open top could lead to some embarrassment!

Using computer models can give you an inaccurate result, with perhaps MCNP (Monte Carlo) coming closest to what you might measure in reality. However, when using these models at the 'limit' (e.g. very near the shielding wall), real measurement data will be more reliable in most cases. And so for the above example, using experience of similar real life shielded sources, the dose rate on the wall surface will be substantially less than the 18 micro Sv/h measured at 2m. It will most likely tend towards <1 micro Sv/h.

Furthermore, again from experience of real-life shielding, the dose rate of 18 micro Sv/hour at 2m will be the likely maximum and this will then tend to reduced with increasing distance. This is how sky-shine can lead to unintended exposures where measurements are first taken at the wall (yielding low dose rates) and then at a significant distance away from the shield (also yielding low dose rates). You may well have missed the peak!

In the above example, moving from 2m to 4m away from the wall will reduce the dose rate to about 14 micro Sv/h. This reduction clearly shows that the inverse square law is irrelevant.

If you think you may have a sky-shine issue, or need practical advice regarding radiation shielding (particularly where you have an open top shielding bunker) then feel free to contact the Ionactive Radiation Protection Adviser (Mark Ramsay).