Distance travelled by Beta Particles in air and other materials

Published: Sep 29, 2021

The rule of thumbs

The distance a beta particle will travel in air (its range) is given by: Range_air = 3.7 m per MeV

The E_max for P-32 is 1.71 MeV. Therefore the maximum range in air with no other shielding medium would be 6.3 m. This might come as a surprise, but it should be noted this is E_max, so its the absolute maximum range of a P-32 beta particles (the intensity of beta particles will be much less than at the average distance).

The average energy of a beta particle can be expressed as E_ave (beta) = 1/3 E_max (beta)

Therefore, the E_ave (beta) for P-32 should be about 0.57 MeV (its actually 0.695 MeV from resource tables). Its a reasonable approximation to show that the average distance (peak number of beta particles) is more like 2.1 m (average energy approximation) or 2.57 m (for known average beta energy).

So far we have only considered the distance that beta particles will travel through air. In order to provide a rules of thumb to cover all other materials it is advantageous to consider distance (range) in terms of the g/cm² or (mg/cm²). Where the range is given in g/cm², the linear thickness of a particular material can then be determined by division of the materials density (in g/cm³). A very simple relationship is then as follows.

The range (R) of beta particles in matter rules of thumb is given by R (g/cm²) = E_max / 2

The density of air at standard temperature and pressure is 0.001225 g/cm³. Using this expression for P-32 (beta max energy is 1.7 MeV), we find that R (g/cm²) = 1.7/2 = 0.85. We can then covert this to distance by dividing by the density of air. Therefore 0.85 g/cm² / 0.001225 g/cm³ = 693 cm = 6.9 m. Whilst not exactly the same, this compares well with the 6.3 m calculated above using Range_air = 3.7 m per MeV. This simple rules of thumb is reliable enough for workplace radiation safety where E_max is in the range of 1-4 MeV.

If you would like to use a more sophisticated rules of thumb for beta distance in any particular material then you need to use expressions based on curve fitting of beta max energy (MeV) against range (distance) in mg/cm³. More than one rule is required in order to provide a best 'fit' for each part of the curve.

The range (R) of beta particles in matter rules of thumb (from curve fitting) are given by R(mg/cm²) as follows:

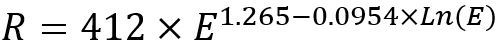
(0.01 ≥ E ≥ 2.5 MeV)

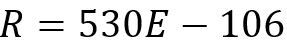
(where E > 2.5 MeV)

The value of E in the above expressions represents E_max (maximum beta particle energy in MeV).

The distance beta particles travel in materials - discussion

Using the curve fitting rules of thumb we can compare range in air with similar expressions given previously. Using P-32 we can calculate the range based on an E_max of 1.71 MeV. The equation for this will look like the following:

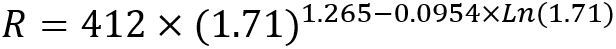
The calculation shows that R = 790 mg/cm².

The density of air is 1.225 mg/cm³ and therefore the maximum range of P-32 beta particles in air is shown to be 645 cm (6.45 m) by dividing the value calculated for R by the density of air.

This result is pretty close to the values calculated above, being nearly identical to the 'Range_air = 3.7 m per MeV' rule of thumb (which was 6.3 m).

If we perform the same calculation for C-14 (E_max of 0.156 MeV), we will find that the maximum distance in air is 23 cm.

Using the beta range rule of thumb to demonstrate beta shielding performance

It is often said that 10 mm of perspex, Poly(methyl methacrylate), is ideal for protection against beta radiation from common beta emitters found in the workplace. The choice of perspex serves three main purposes:

The perspex offers a near 100% reduction in beta radiation (i.e. near enough 100% shielding)
The use of low density shielding reduces the production of bremsstrahlung (x-ray) radiation (see rules of thumb on beta bremsstrahlung)
The use of a transparent shield, particularly in laboratory situations, provides clear viability when working with beta emitters

A common high energy beta emitter used in the workplace is P-32 as already featured above. We can use the above equation to investigate the P-32 beta range in perspex and see if the 10 mm thickness is justified.

The value of R, for P-32, was shown to be 790 mg/cm². The density of perspex is 1180 mg/cm³. Recall that we need to take the value of R, and divide by the density of perspex which gives us 0.7 cm (7 mm). Therefore, 10 mm of perspex seems a safe bet.

Now consider much higher energy beta emitter, Sr-90. The beta emission from Sr-90 is only 0.54 MeV, however its daughter is Y-90 and this has a beta max of 2.27 MeV. Therefore we need to protect against the Y-90 beta emission when using Sr-90.

Using the above equation, we see for Sr-90 (Y-90) that the value of R = 1090 mg/cm².

Noting the density of perspex is 1180 mg/cm³, and dividing into the value of R, we see that the thickness should be 0.92 cm (9.2 mm). Therefore even for higher energy beta emitters, 10 mm of perspex should provide 100% beta attenuation with minimal bremsstrahlung. [Bremsstrahlung from beta particle interaction with matter will be demonstrated in a separate rules of thumb article].